Boniface
There are some things that, in the course of normal query writing, just can’t be SARGablized. For example, generating and filtering on a windowing function, a having clause, or any other runtime expression listed here.
There are some interesting ways to use indexed views to our advantage for some of those things. While windowing functions and having clauses can’t be directly in an indexed view, we can give an indexed view a good definition to support them.
I Don’t Care For It
Starting with these indexes to help things along, they don’t really do as much as we’d hope.
CREATE INDEX c ON dbo.Comments (PostId); CREATE INDEX v ON dbo.Votes (PostId); CREATE INDEX p ON dbo.Posts (Id, OwnerUserId, Score);
This query has to process a ton of rows, and no matter what we set the having expression to, the entire result set has to be generated before it can be applied. We could set it to > 0 or > infinity and it would take the same amount of time to have a working set to apply it to.
SELECT
p.OwnerUserId,
TotalScore =
SUM(ISNULL(p.Score * 1., 0.)),
records =
COUNT_BIG(*)
FROM dbo.Posts AS p
JOIN dbo.Comments AS c
ON c.PostId = p.Id
JOIN dbo.Votes AS v
ON v.PostId = p.Id
GROUP BY
p.OwnerUserId
HAVING
SUM(ISNULL(p.Score * 1., 0.)) > 5000000.
ORDER BY
TotalScore DESC;
Limited Liability
I know that having clause looks funny there, but it’s not my fault. The sum of Score ends up being a really big integer, and overflows the regular sized integers unless you explicitly convert it to a bigint or implicitly convert it to something floaty. The isnull is there because the column is NULLable, which is unacceptable to an indexed view.
So, here we are, forced to write something weird to conform.
Sizzling. Sparkling.

Ignoring the woefully misaligned and misleading operator times, we can see in the query plan that again(!) a late Filter operator is applied that aligns with the predicate in our having clause.
Sarging Ahead
Let’s work some magic, here.
CREATE VIEW
dbo.BunchaCrap
WITH
SCHEMABINDING
AS
SELECT
p.OwnerUserId,
TotalScore =
SUM(ISNULL(p.Score * 1., 0.)),
records =
COUNT_BIG(*)
FROM dbo.Posts AS p
JOIN dbo.Comments AS c
ON c.PostId = p.Id
JOIN dbo.Votes AS v
ON v.PostId = p.Id
GROUP BY
p.OwnerUserId;
GO
CREATE UNIQUE CLUSTERED INDEX bc ON dbo.BunchaCrap(OwnerUserId);
This gives us an indexed view with the TotalScore expression materialized, which means we can search on it directly now without all the 50 some-odd seconds of nonsense leading up to it.
At The Mall
Our options now are either to query the indexed view directly with a noexpand hint, or to run the query as initially designed and rely on expression matching to pick up on things.
SELECT
bc.*
FROM dbo.BunchaCrap AS bc WITH (NOEXPAND)
WHERE bc.TotalScore > 5000000.
ORDER BY bc.TotalScore DESC;
In either case, we’ll get this query plan now:
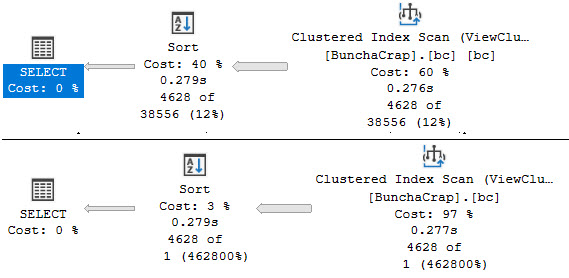
Which looks a whole heck of a lot nicer.
Tomorrow, we’ll look at how implicit conversion can look a lot like non-SARGable predicates.
Thanks for reading!
Going Further
If this is the kind of SQL Server stuff you love learning about, you’ll love my training. I’m offering a 75% discount to my blog readers if you click from here. I’m also available for consulting if you just don’t have time for that and need to solve performance problems quickly.
Do you have any tips/tricks to implement an indexed view on top of tables that already exist without locking them up? ONLINE = ON is not an option for creating a new clustered index on a view.
They don’t get locked up, check out this post by Kendra: Does Creating an Indexed View Require Exclusive Locks on an Underlying Table?
Interesting. I thought I’d run into concurrency issues in trying to create an indexed view in the past, but figured I’d give it a try again. On a test system, I created a simple view whose definition was “select * from mytable where ID < 10000000" and put a unique clustered index on it. In another session I attempted to insert a new value into the table and was blocked by the index creation process. Looking at the blocking info, it says that the insert was waiting on Sch-M ("objectlock lockPartition=27 objid=573245097 subresource=FULL dbid=21 id=lock1b1c475c700 mode=Sch-M associatedObjectId=573245097" where 573245097 is the object_id of the view).
I'll look into this more in a little bit.
Greetings again… from the FUTURE!
I came back to this while testing adding an indexed view to an existing table. I have a repro of the observed behavior with the StackOverflow2010 db. If I change the view definition to
CREATE OR ALTER VIEW dbo.IndexMe
WITH SCHEMABINDING
AS
SELECT
OwnerUserID ,
PostTypeId ,
COUNT_BIG(*) as CT
FROM dbo.Posts
GROUP BY
OwnerUserID ,
PostTypeId;
GO
And changed the index on the view accordingly. My query is:
SELECT
PostTypeId ,
COUNT(*) as CT
FROM dbo.Posts
WHERE OwnerUserId = 8
GROUP BY
PostTypeId;
To simulate the contention I’d see on a much larger table, I put the create index in a transaction and left it uncommitted. When I run the query, it’s waiting on a schema mod lock on the view and therefore blocked. It’s unclear to me why the optimizer is considering the view before the index creation is complete but there you have it.
Ooh, that’s a lot of fun!
I’d say it’s Type 3 fun but would be willing to concede Type 2.
I don’t suppose you have any Consultant Trix™ to get around that behavior?